Computing leaky waves in semi-analytical waveguide models by exponential residual relaxation
Gravenkamp, H., B. Plestenjak, and D. A. Kiefer
Computer Methods in Applied Mechanics and Engineering 452, 118763 (2026)
Résumé: Semi-analytical methods for modeling guided waves in structures of constant cross-section yield frequency-dependent polynomial eigenvalue problems for the wavenumbers and mode shapes. Solving these eigenvalue problems over a range of frequencies results in continuous eigencurves. Recent research has shown that eigencurves of differentiable parameter-dependent eigenvalue problems can alternatively be computed as solutions to a system of ordinary differential equations (ODEs) obtained by postulating an exponentially decaying residual of a modal solution. Starting from an approximate initial guess of the eigenvalue and eigenvector at a given frequency, the complete eigencurve is obtained using standard numerical ODE solvers. We exploit this idea to develop an efficient method for computing the dispersion curves of plate structures coupled to unbounded solid or fluid media. In these scenarios, the approach is particularly useful because the boundary conditions give rise to nonlinear terms that severely hinder the application of traditional solvers. We discuss suitable approximations of the nonlinearity for obtaining initial values, analyze computational costs and robustness of the proposed algorithm, and verify results by comparison against existing methods.
|
|
Laser ultrasonic investigation of chromium coating impact on elastic guided waves in zirconium tubes
Diboune, H., D. A. Kiefer, F. Lyonnet, P. Barberis, F. Bruno, S. Mezil, and C. Prada
Journal of the Acoustical Society of America 159, no. 1, 398-407 (2026)
Résumé: The impact of a chromium (Cr) coating on the elastic guided waves propagating in zirconium alloy (called M5 Framatome and referred to as M5 hereafter) nuclear cladding tubes is studied both theoretically and experimentally. Longitudinal modes are measured on different 9.5 mm-diameter tubes by a non-contact laser ultrasonic technique. These modes are calculated using the M5 elastic constants determined from x-ray diffraction measurements. Since Cr has a much higher shear wave velocity than the M5 alloy, the dispersion of observed guided modes is significantly modified by the coating. In the mid-frequency range, characterized by shear wavelengths on the order of the tube thickness, the second longitudinal mode appears to be particularly sensitive to the coating. In a higher frequency range, it is observed that modes are well measured in a frequency-wavenumber domain corresponding to the leaky surface wave of a Cr coated infinite M5 substrate. A simple but effective model predicts the observability of each mode, in good qualitative agreement with experimental observations.
|
|
Entropy-controlled velocity-dependent behavior of landslide clayey soil across a wide velocity range
Hu, W., Y. Zheng, Y. Ge, L. Zhou, Y. Li, and X. Jia
Earth and Planetary Science Letters 671, 119671 (2025)
Résumé: The shear resistance of the shear zone governs the behavior of many landslides. Among the factors influencing shear resistance, the velocity dependence of the shear zone can give rise to rapid catastrophic failure (velocity-weakening) or exert a deceleration effect (velocity-strengthening). In this study, we investigated the shear-velocity dependence of shear zone in clayey soil from the Baige landslide in Tibet, China, across a broad range of velocities (3.3 × 10<sup>−8</sup> to 6 m/s), at typical landslide stress levels (200 to 2000 kPa), to simulate the whole lifespan of the landslide, from creep deformation to rapid catastrophic failure. We found that the shear velocity dependence of clayey soils could be classified into three regimes: slight weakening at slow velocities, substantial velocity-strengthening at intermediate velocities, and rapid weakening at high velocities once a critical velocity was attained. The mechanisms for the first and second regimes were explained by the alignment (entropy) change of clay particles along the shear surface. At very slow shear velocities, clay particles become aligned parallel to the shear surface, causing slight weakening and a drop in entropy. As the shear velocity increased, the clay particles became less aligned and more randomly distributed, interlocking with each other, giving rise to strong velocity-strengthening. The rapid weakening in the third regime was associated with frictional heating, independent of entropy. Across the slow to intermediate velocity range, clay particle entropy controls velocity-weakening and velocity-strengthening frictional behavior of shear zones, potentially influencing landslide slow creep. In contrast, rapid shearing causes frictional weakening in clayey shear zones, which may trigger landslide rapid failure. This study offers new insights into landslide dynamics and the transition from creep to rapid failure.
|
|
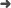
Reconfigurable and active time-reversal metasurface turns walls into sound routers
Dorlot, F., C. Bourdeloux, M. Fink, and F. Lemoult
Communications Physics 8, no. 1 (2025)
Résumé: Sound control in noisy or reverberant spaces is important for applications ranging from communication to immersive audio. However, existing methods often struggle to deliver sound selectively to specific listeners without interference. Here we show that an active acoustic metasurface, composed of programmable elements that both sense and re-emit sound, enables precise targeting of audio in complex environments. Each element processes signals in real time using convolution filtering, allowing us to exploit reciprocity and time-reversal symmetry in wave propagation. Experiments with audible sound in reverberant rooms demonstrate that this approach creates clear, individualized sound channels while suppressing unwanted noise. This research opens new possibilities for adaptive sound delivery in crowded or dynamic settings, with potential applications in conferencing, entertainment, and assistive listening technologies.
|
|
